対数

対数の定義: aとb は正の実数であり、 a ≠ 1であるため、 a ^xの累乗がbに等しくなるように底aを累乗する必要がある指数xは、 aを底とするbの対数と呼ばれます。

log _a b = x ↔ a ^x = b

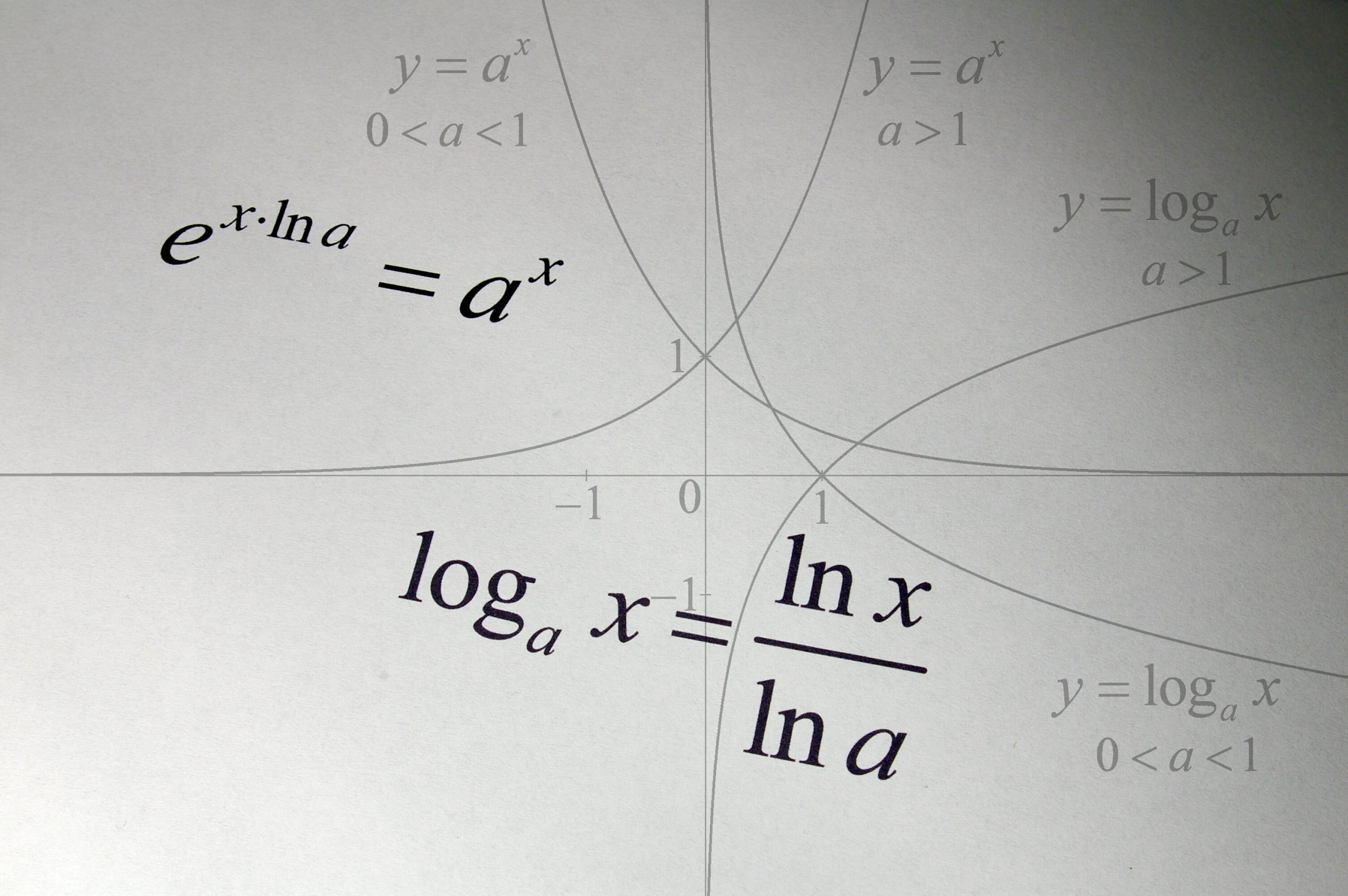
log _a b = x という式では、次のようになります。
• a は対数の底です
• b は対数です
• x は対数です。

対数の例をいくつか見てみましょう。

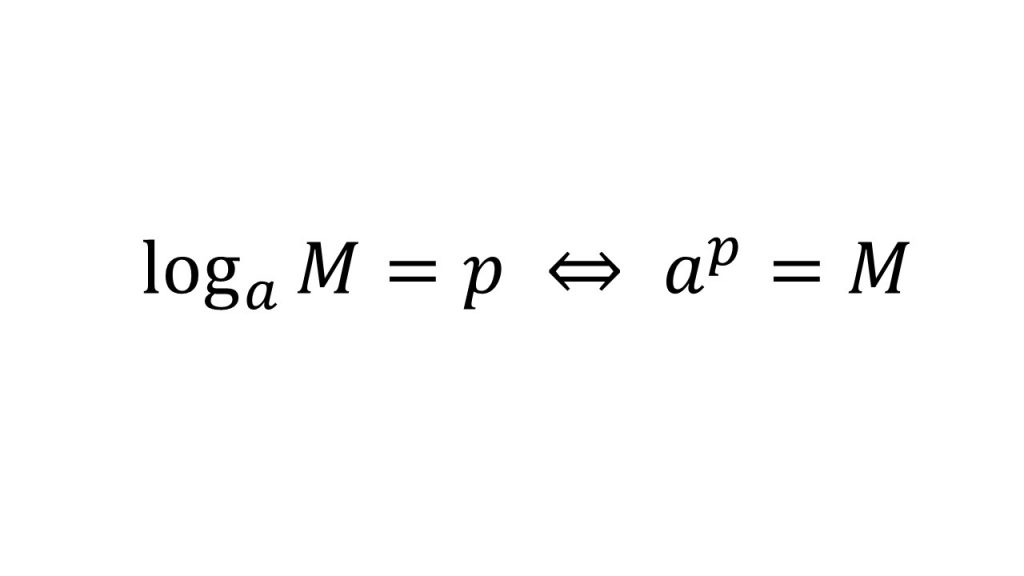
定義に従って計算してみましょう。

結果：
対数の定義から、次の特性が得られます。

第 1 任意の底 a の 1 の対数は 0 に等しい。
a ⁰ = 1 なので、log _a 1 = 0 となります。

2 底の対数は、それが何であっても 1 に等しい。
a ¹ = a であるため、log _a a = 1

3番目 底aと指数log _a bのべき乗はbに等しい。
a ^{log _a b} = b です。底aのbの対数は、べき乗がbと等しくなるように底に与える必要がある指数です。

例: 5 ^{log ₅ 7}の値を計算してみましょう
5^{対数₅ 7} = 7

4 番目 同じ底の 2 つの対数が等しい場合、その対数も等しい。
log _a b = log _a c → b=c

このテーマに関するビデオレッスンをぜひご覧ください。