円は、中心点Oと距離rが与えられた場合、点と中心点Oの間の距離がr以下でなければならない点の集合です。
つまり、円は、次の図に示すように、境界として円周を持つ平らな領域です。
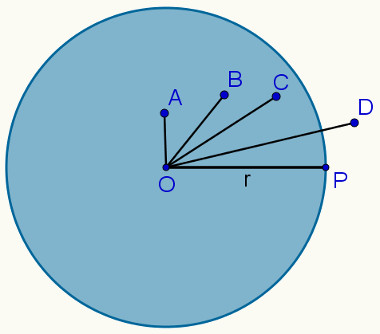
上の円では、それに属するいくつかの点とその外側の 1 つの点が強調表示されています。これらの点のどれが円に属しているかを理解するには、単に円の端と中心点の間の距離であるrより小さい距離を持つ点を判断するだけです。
したがって、2 点間の距離は、2 点を結ぶ直線の長さになります。このセグメントが円の端と交差するとき、その端の点はこの図の外側になります。これが起こらない場合、その点は円に属します。上の例では、円上の点は O、P、A、B、C です。円に属さない唯一の点は D です。
円要素

→ 半径
円の中心と端の間の距離です。この定義では、これはrの尺度であり、通常はこの文字で表されます。

→ 直径
円の端上の 2 点を結び、その中心を通過する直線セグメントです。このようにすると、直径は常に半径の 2 倍のサイズになります。

→ 長さ
円の長さ (周長とも呼ばれます) は、それを制限する円周の長さに等しく、次の式で取得できます。
C = 2・π・r
π には固定値 (約 3.14 に等しい) があるため、円の半径の長さからその長さを計算することができます。
→円の面積
円の面積は、平面内で占める空間の量であり、次の式を使用して取得できます。
A = π・r 2
したがって、円の半径がわかれば、その面積を求めることができます。

→ 円形扇形
扇形は、2 つの半径によって決定される円のスライスです。たとえば、次の図の明るい部分は円形の扇形で、暗い部分は別の円形です。
最も明るい円形セクターも斜めに強調表示されていることに注意してください。この角度から、扇形 (x) の面積を求めることができます。これを行うには、単純に3 の法則で円の合計面積 (A = π・r2) と円の合計角度 (360°) を使用します。このようにして、次のようになります。
π r 2 = 360
×α
360x = α・π・r 2
x = α・π・r 2
360
したがって、3 の法則または上記の式を使用して、扇形の面積を決定できます。
1 番目の例– 半径 25 センチメートルの円の面積と周囲長を計算します。
解決策: 半径は 25 cm なので、この値を面積と長さ (円の周囲長) の式に代入します。これらの計算では、π が 3.14 にほぼ等しいことに注意してください。
A = π・r 2
A = 3.14・25 2
A = 3.14・625
A = 1962.5cm 2
2 番目の例– 中心角が 90°である扇形の面積を計算します。
解決策: 扇形の面積を表す x に対して得られた式を使用します。
x = α・π・r 2
360
x = 90・3.14・25 2
360
x = 3.14・625
4
x = 1962.5
4
x = 490.6 cm 2程度です。
90°は 360°の 4 分の 1 であることに注意してください。したがって、扇形の面積は円の面積の 4 分の 1 でなければなりません。
このテーマに関するビデオレッスンをぜひご覧ください。

.jpg)